仮定を使って、その図形が平行四辺形であることの証明をする。その後平行四辺形の条件を使って結論を出す。というやり方ですね。 ちなみに今回の結論は条件①ですね。 1 菜々美 4 เดือนที่แล้ว 丁寧な説明ありがとうございます☺️ 0 แสดงความคิดเห็น辺=辺 ① 辺=辺 ② 辺=辺 ③ 平行四辺形の証明の練習問題3 平行四辺形abcdで, 対角線の交点oを通る直線を,右の図のようにひき, 2辺ab, cd との交点を, それぞれ, p, q とします。このとき, op=oq となることを証明し

中2数学 長方形 ひし形 正方形 映像授業のtry It トライイット
平行四辺形 証明 解き方
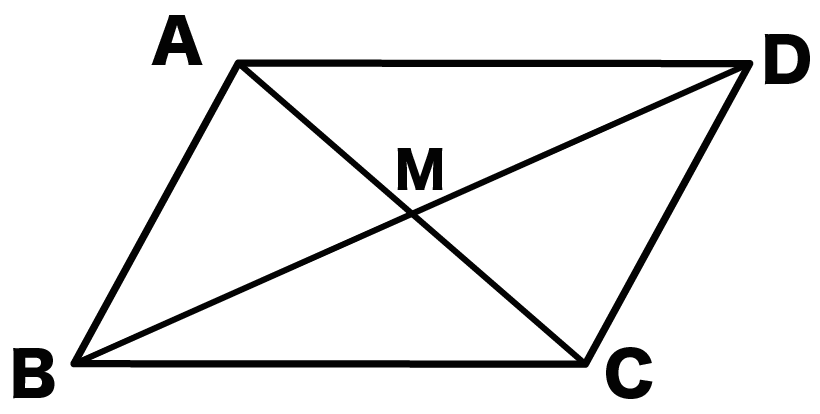
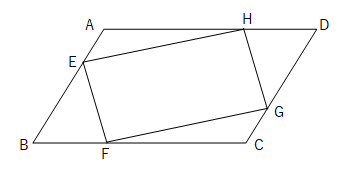
平行四辺形 証明 解き方- 中点連結定理で平行四辺形を証明する3つのステップ さっそく証明問題をといていくよ。 四角形ABCDの4辺AB、BC、CD、DAのそれぞれの中点をE、F、G、Hとする。 このとき四角形EFGHが平行四辺形になることを証明しなさい。 Step1 対角線をひく 証明2 2組の向かいあう辺が、それぞれ等しい。 abcと cdaで、 ab=cd 1 bc=da 2 ac=ca(共通) 3 1,2,3より3辺がそれぞれ等しいので、




7の解き方と答え教えて頂きたいです Clear
加減法の解き方(標) 代入法の解き方(標) 加減法の練習(基) 加減法の練習(標1) 加減法の練習(標2) 代入法の練習(基) 代入法の練習(標1) 代入法の練習(標2) ≪トップ≫ 連立方程式② 小数係数の方程式; 平行四辺形の定義と性質・証明問題の解き方 管理人 2月 23, 19 平行四辺形の性質で角度を求めたり、平行四辺形であることを証明したりする問題がよく出されます。こんにちは、ウチダショウマです。 今日は、中学2年生の内容である 「平行四辺形になるための5つの条件」 について、平行四辺ウ 上の証明から,すべての平行四辺形で,2組の向かい合う辺はそれぞれ等しいことが分かる。 エ 上の証明から,台形の2組の向かい合う辺はそれぞれ等しいことも分かる。 2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ③ 3 下の図のような
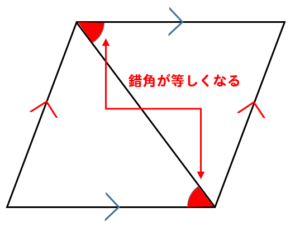
(2)次の四角形abcdが平行四辺形のとき および をもっとも簡単な整数比で求めなさい。 解き方 平行線が作る2つの三角形は相似になります。 平行条件 ・錯覚が等しい ・同位角が等しい で、平行四辺形の証明はなんとかなると思います。 補 つまり 平行四辺形であることを証明する →何の条件を以てして平行四辺形であることを証明するか →「2組の対辺がそれぞれ平行である」を示せればよい →平行であることを証明しなければならない →何の条件を以てして平行であることを証明するか →「同位角金銭問題(基) 数の問題(基) 割合の問題(標) 食塩濃度(標) 速度
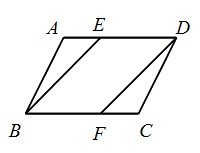
相似と線分比1(平行四辺形) abcdでaeeb=13, bffc=21のとき eggdの線分比を求めよ。 a b c d e f g正三角形ならば、三辺が等しいのも仮定です。 AB=CDという仮定を見つけたら、辺上に「〃」のマークを付けるなどします。 正三角形なら、3つの角が60度で等しいですね。 ∠ABC=∠DEFを見つけたら、同じように印を付けておきましょう。 マーカーで色分けするのもOKです。 このように印をつけると、証明(証明の進め方) ※他の形になる場合も,直線 l に平行な直線をひけば同様にして示せる. 例題1 直線 l が abc の3辺またはその延長と右図のように, p, q, r で交わるとき, bccq を最も簡単な整数の比で表してください. (解答)(メネラウスの定理を覚えている場合) メネラウスの



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
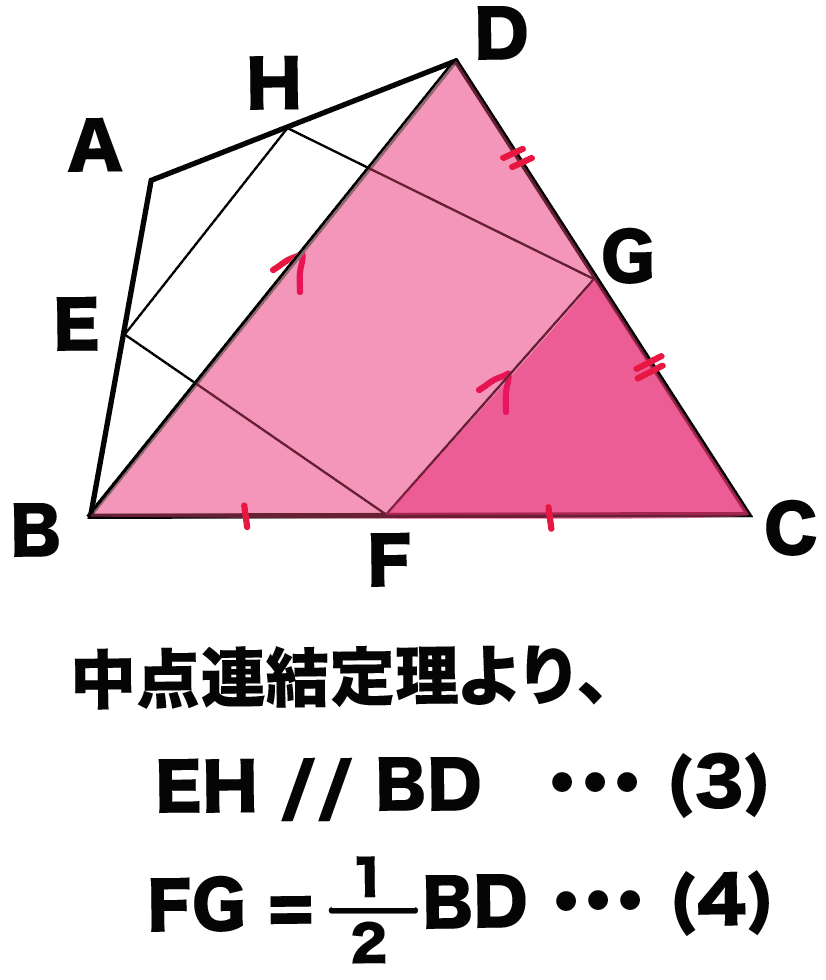



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
平行四辺形の面積は、\(8\times 5=40\)となります。 よって、この平行四辺形の面積は\(40cm^2\)となります。 平行四辺形の面積の公式が、底辺×高さとなるのはなぜか 平行四辺形の面積の公式が底辺\(\times\)高さになる理由をみていきましょう。 ・2枚の平行四辺形を使って平行四辺形の特徴を調べる。 2 ・平行四辺形のかきかたを考え、かく。 1 ・ひし形の性質を考え、かく。 1 ・いろいろな四角形の対角線の特徴をまとめる。 1 ・長方形や平行四辺形の1本の対角線で切り、できた2つの三角形を調べる。 まとめ 3 1 平行と線分比の考え方を、特別な図形のときに限定して便利にしたもの ということがわかってもらえるかと思うんじゃな トンちゃん え、どういうことですか? メネラウスの定理というのは、平行と線分比の考え方の一部、ということなんじゃ トンちゃん なるほどです! といっても具体




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学




平行四辺形の定義と性質 証明問題の解き方 数学fun
平行四辺形の証明のコツってありますか? 数学 中学生 1年以上前 n 平行四辺形の証明のコツってありますか? 0 回答 ベストアンサー ゆいな 1年以上前 全部においてかもしれませんが、 等しいところを全部図にかいてから解くと わかりやすいですよー 2 n 1年以上前 ありがとうござい (1)は、平行四辺形のときと考え方は同じです。縦の線を2本、横の線を2本選ぶことと、長方形とが対応します。縦の線が5本あって横の線が4本あるので、線の選び方の式は先ほどと同じで\ {}_5 \mathrm{ C }_2 \times {}_4 \mathrm{ C }_2 = 10 \times 6 = 60 \通り、となり、長方形の個数は60個となります。 三角形の内角の和が180°であること、直線が180°であることを利用します。 平行四辺形(1) 平行四辺形と直角三角形のパターンです。 直角三角形の合同と錯角を利用します。 平行四辺形(2) 平行四辺形を対角線を利用して証明するパターン。




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear




至急 たしかめ2と問5の証明教えて下さい Clear
平行四辺形の定義と性質・証明問題の解き方 管理人 2月 23, 19 平行四辺形の性質で角度を求めたり、平行四辺形であることを証明したりする問題がよく出されます。こんにちは、ウチダショウマです。 今日は、中学2年生の内容である 「平行四辺形になるための5つの条件」 について、平行それぞれの特徴を比較! そもそも平行四辺形とは このように 向かい合う辺がそれぞれ平行になっている四角形 のことを平行四辺形といいます。 更に、次のような条件を満たす四角形はすべて平行四辺形ということができます。 平行四辺形になるための条件 2組の対辺がそれぞれ平行である。 2組の対辺がそれぞれ等しい。 2組の対角がそれぞれ等しい 下図(34枚目のスライド)を見て欲しい.行列 A の1列目が橙色ベクトル,2列目が緑色ベクトルだったが,これらはそれぞれ,x 軸方向と y 軸方向の単位ベクトルを行列 A で線形変換してできるベクトルだ.つまり,各辺の長さが 1 の正方形(紫色)を平行四辺形(水色)に変形するの



平行四辺形になるための証明1



平行四辺形になるための証明1
数学の証明問題を攻略するための6つのコツ つぎの例題をときながら解説するよ。 AB = DC、AB // DCの ABCと CDAがあったとします。 このとき、角ABC = 角CDAであることを証明しなさい。 コツ1 「仮定」と「結論」をみつける! 数学の証明問題でいちばん最初にやることは、 仮定と結論 をみつけてやることさ。 仮定とは、カンタンにいってしまえば、 証明問題の解き方の流れ ここからは証明問題の解き方の流れを具体的に解説します。 証明するための条件選び 合同の証明には以下3パターンの条件のいずれかを用います。 三組の辺がそれぞれ等しい;三平方の定理(ピタゴラスの定理)の公式と計算方法 中点連結定理と相似:定理の逆や平行四辺形の証明、応用問題の解き方 中学数学の三角形の相似:相似条件・図形の証明と相似比・面積比 平行四辺形の定義・定理(性質)と証明問題:中学数学の図形 二等辺三角形・直角三角形の定義:合同条件と証明問題 三角形の合同条件:合同の証明問題と解き方のコツ



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典
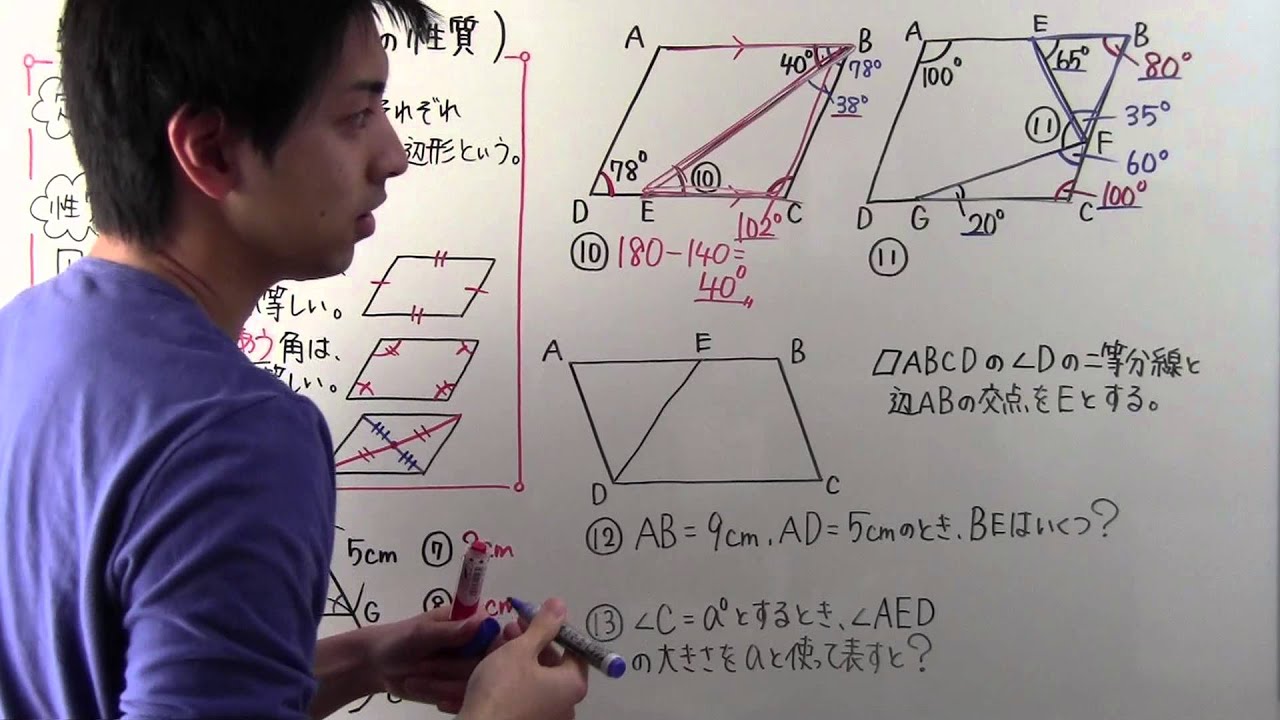



数学 中2 73 平行四辺形の性質 Youtube
解き方云々で解決するのはあまり良いことではないので、しっかりと理解することを心がけましょう。 なんだかんだ基本が大事 、同位角を作れる平行四辺形では、簡単に相似な図形はつくることができます。当然、平行四辺形である、長方形、正方形、ひし形でも同様のことが言えます三角形の面積=底辺×高さ× 1 2 底辺の長さと高さがそれぞれ等しければ面積は等しくなる。 A B C P ABCと底辺BCが共通の PBCがある。 ABCと PBCの面積が等しい場合、両方の三角形の高さが等しいので >>高さ 直線APと直線BCは平行 になる。 >>平行 等積変形 A B C P ABCと等しい面積の PBCを作るには Aを通りBCに平行な線をひき、 >>平行線角, 円, 外接円, 合同, 作図, 幾何, 中線, 平行四辺形, ひし形, 回転, 正方形, 三角形 中学生でも解ける、大学生でも解けない難問。 ジオジェブラの作図機能を使って考えてみよう。 ジオジェブラは正確なので、図に頼らないで、なぜそのことが言えるのかをよく考えてみよう。



中学数学 平行四辺形の証明問題を徹底解説 数スタ




中2数学 長方形 ひし形 正方形 映像授業のtry It トライイット
平行四辺形の定義と性質・証明問題の解き方|数学FUN 中学数学平行四辺形になることの証明・その3 2組の対辺がそれぞれ等しい。 ということは、ちょっと見方を変えると 「2組の向かい合う辺がそれぞれ等しい」 ってことでもある。 向かい合う2組の辺がそれぞれ平行な四角形• 6em



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
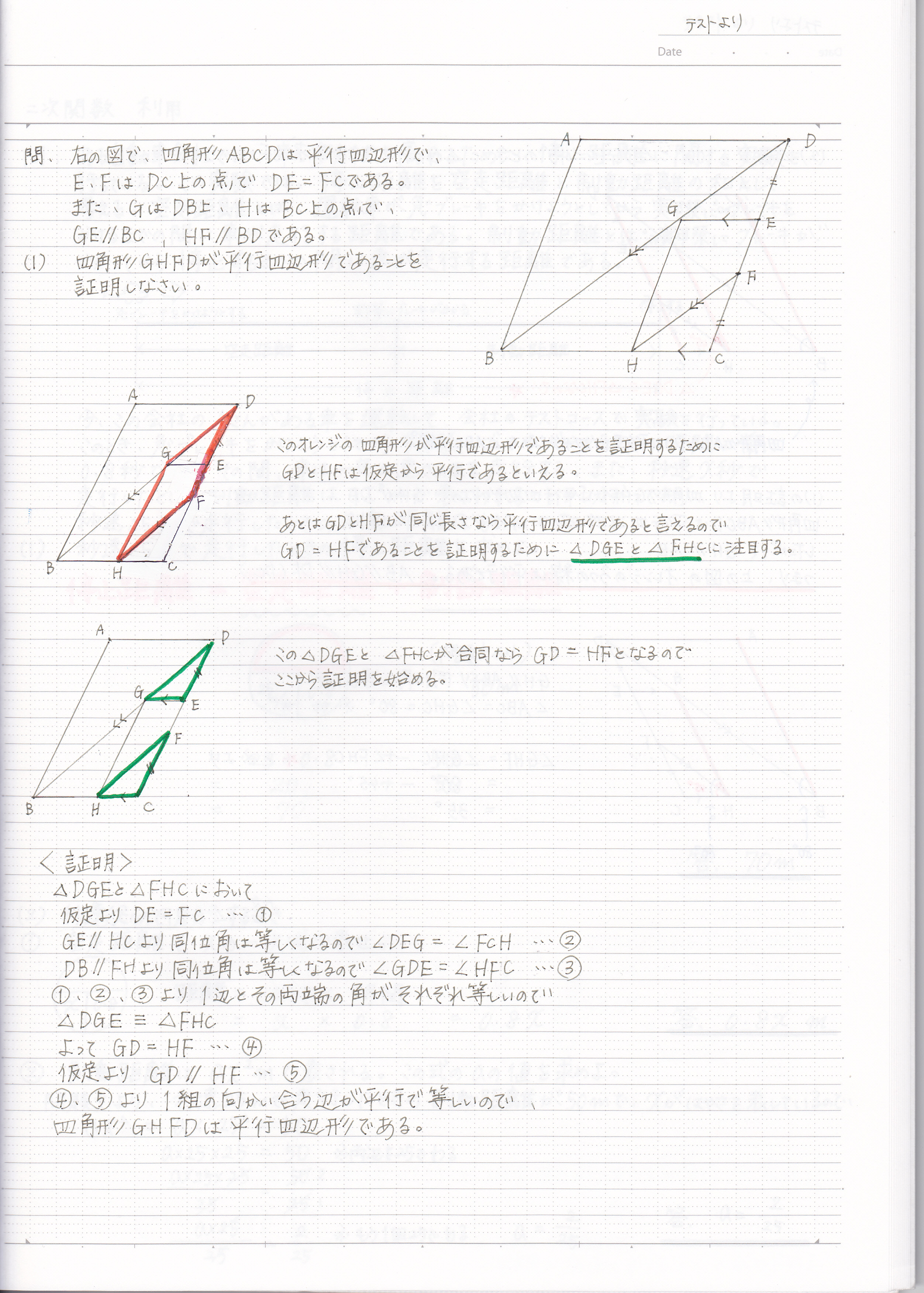



平行四辺形の証明と角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




標準 平行線と平行四辺形の個数 なかけんの数学ノート
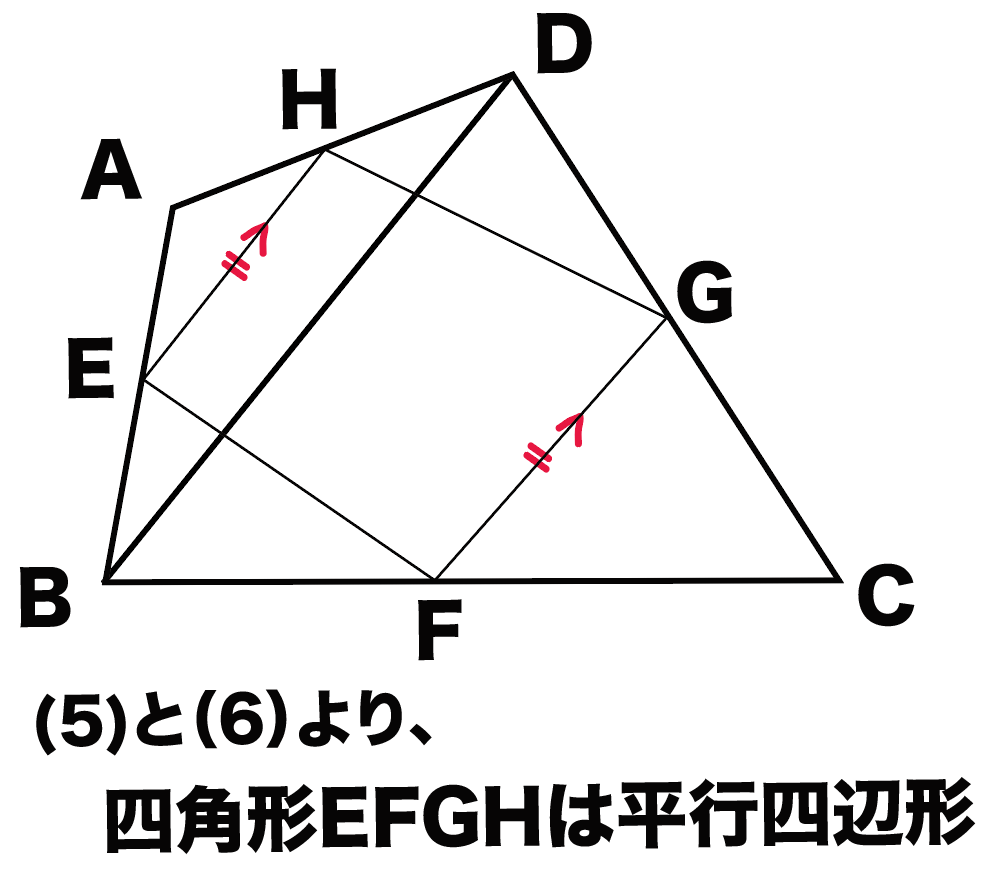



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




中3 19 2 平行四辺形と相似 Youtube
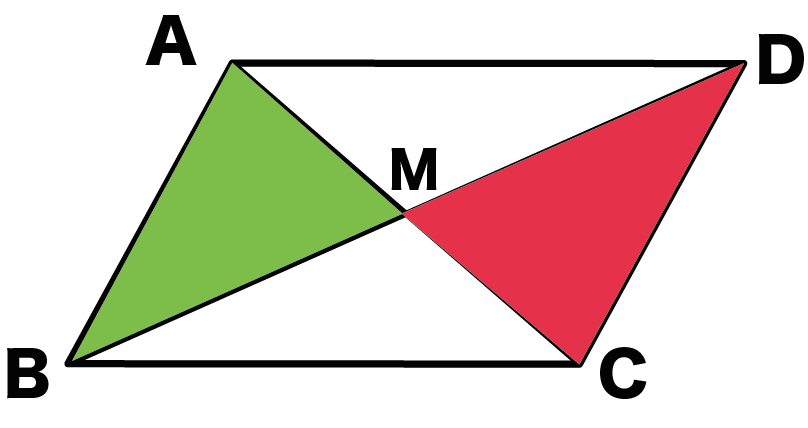



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく



中2数学 証明の問題 Abcdが平行四辺形であることが自明なので Yahoo 知恵袋
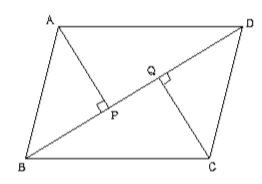



中2数学 平行四辺形の証明のポイントと練習問題 Examee



数学bの問題なんですが平行四辺形abcdでab Adのときac D Yahoo 知恵袋




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル
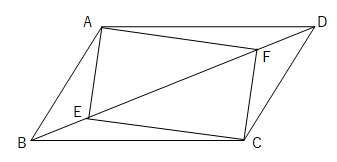



中2数学 平行四辺形の証明のポイントと練習問題 Examee




解き方を教えてください Clear




平行四辺形と証明 Youtube
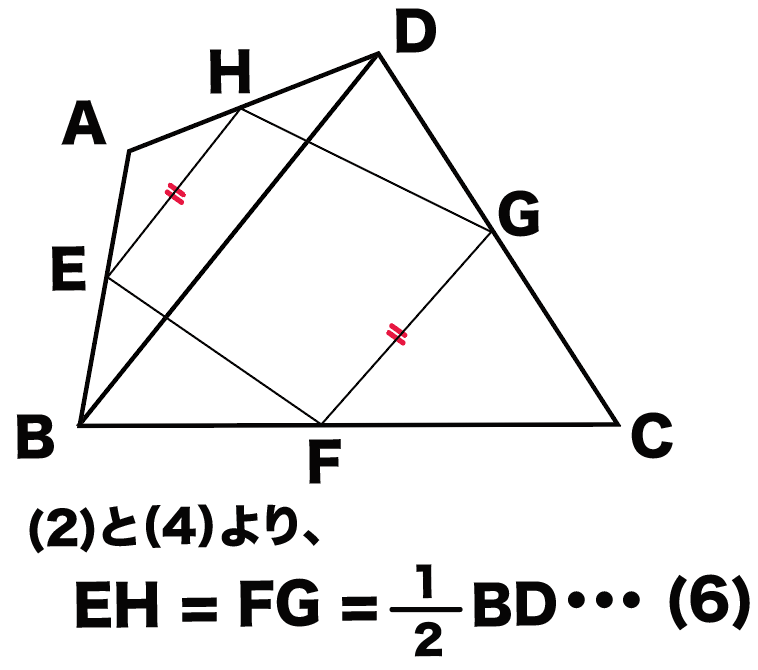



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
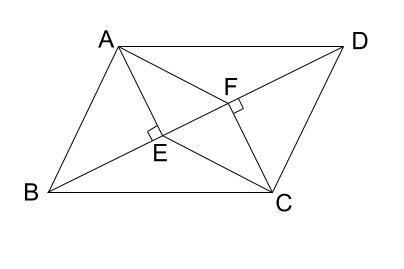



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形の面積の求め方 公式と計算例




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




四角形abcdが平行四辺形 Bfが Abcの二等分線 Abfの面積が6cm のとき Clear
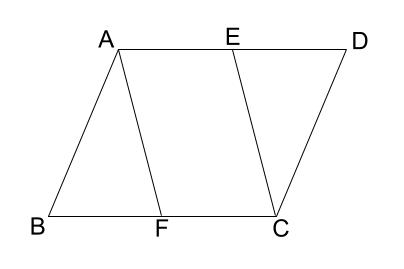



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




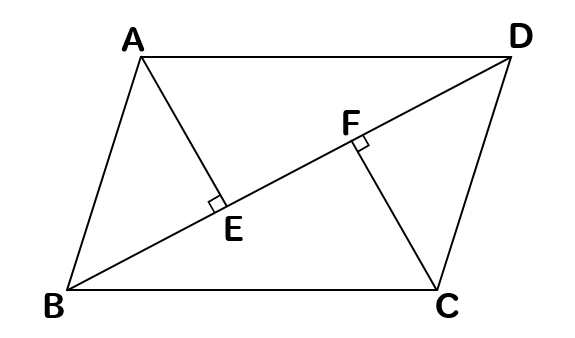
平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



Math 平行四辺形 平行四辺形になることの証明 働きアリ




7の解き方と答え教えて頂きたいです Clear



中2数学 平行四辺形の証明のポイントと練習問題 Examee



平行四辺形の定義と性質 証明問題の解き方 数学fun



3




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学



平行四辺形を利用した証明についての質問です この画像の平行四 Yahoo 知恵袋



中学数学 平行四辺形の証明問題を徹底解説 数スタ




至急 1問でもいいので教えて下さい よろしくお願いします Clear



数学の証明の問題です 平行四辺形abcdの外側に 辺ab をそれ Yahoo 知恵袋




平行四辺形になることの証明 Youtube




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
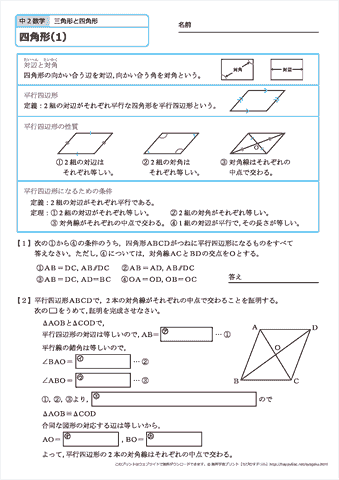



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン



二つの四角形abcd Befcは平行四辺形である このと Yahoo 知恵袋




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方



1
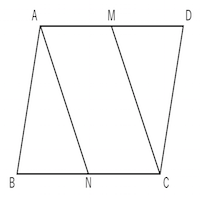



平行四辺形であることを証明する 苦手な数学を簡単に




中2 中2数学 平行四辺形の証明 授業ノート 中学生 数学のノート Clear
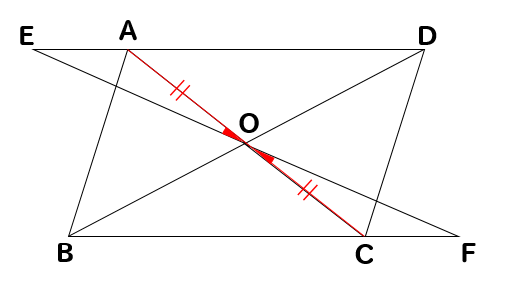



中学数学 平行四辺形の証明問題を徹底解説 数スタ




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



1




中学数学 平行四辺形の証明問題を徹底解説 数スタ




中学数学 平行四辺形の証明問題を徹底解説 数スタ




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
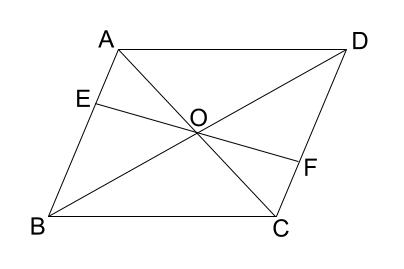



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




Math 平行四辺形 平行四辺形になることの証明 働きアリ
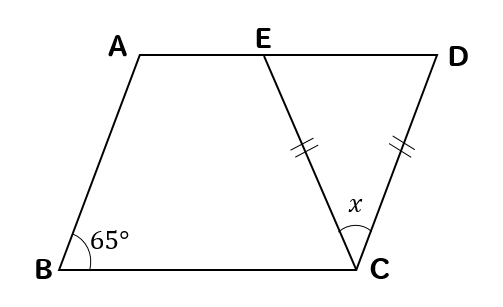



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
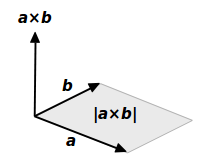



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門



平行四辺形になるための証明1




中2数学 平行四辺形の証明 映像授業のtry It トライイット



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




この問題の答えがあっているのか聞きたいです Clear




平行四辺形の証明 ズバリ解き方はこれ 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




高校数学b ベクトルの成分表示と平行四辺形 受験の月
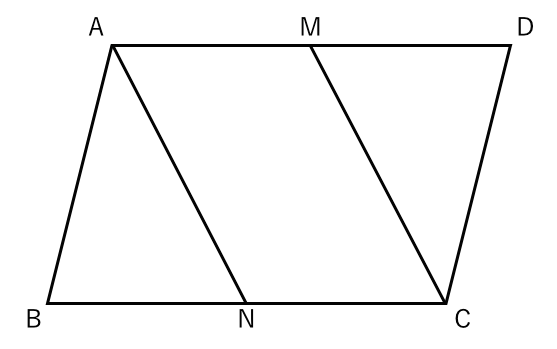



平行四辺形であることを証明する 苦手な数学を簡単に
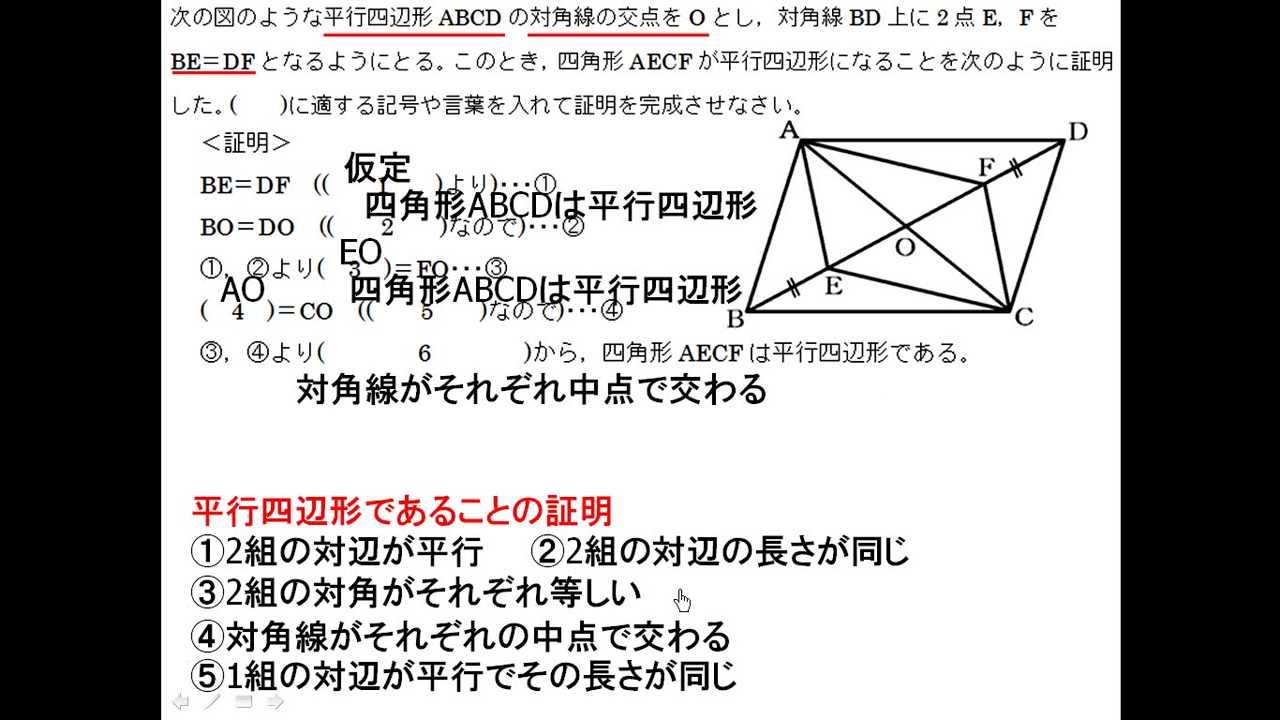



中2 数学 5 3 平行四辺形の証明 Youtube




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学
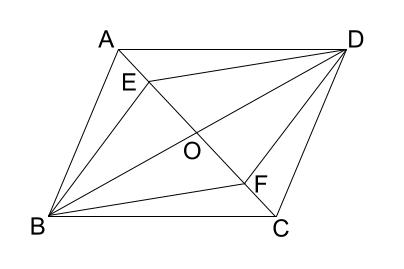



中学数学 平行四辺形になることの証明 その1 中学数学の無料オンライン学習サイトchu Su




平行四辺形の面積の求め方 公式と計算例




数学 中2 74 平行四辺形になる条件 Youtube




平行四辺形の証明問題 無料で使える中学学習プリント




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学
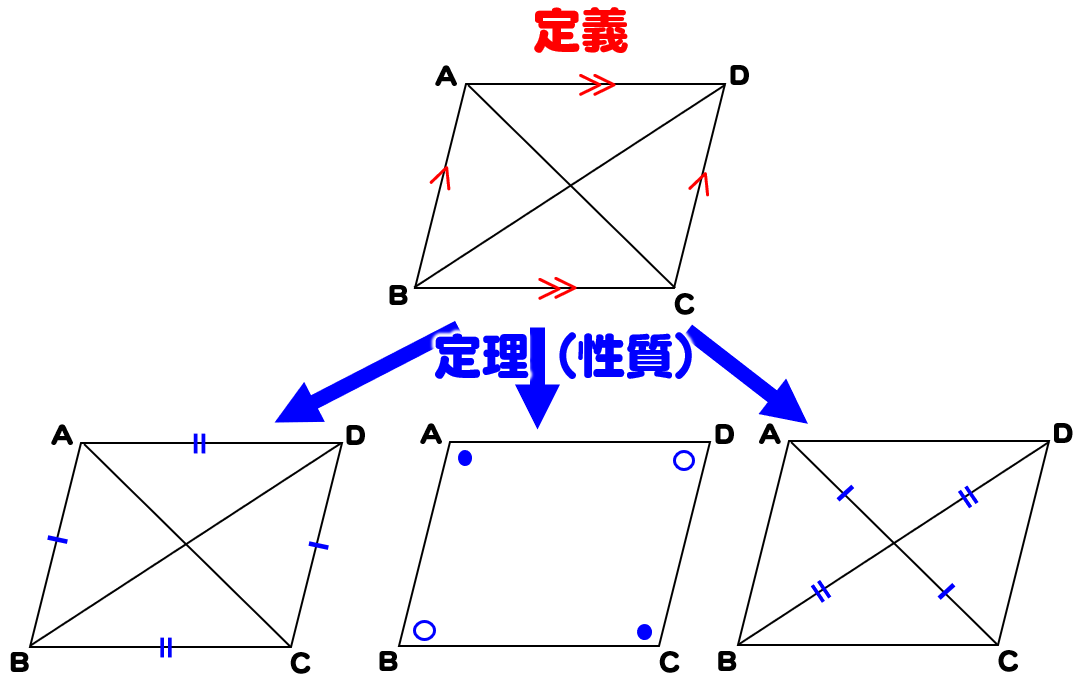



平行四辺形の定義と性質 証明問題の解き方 数学fun




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学
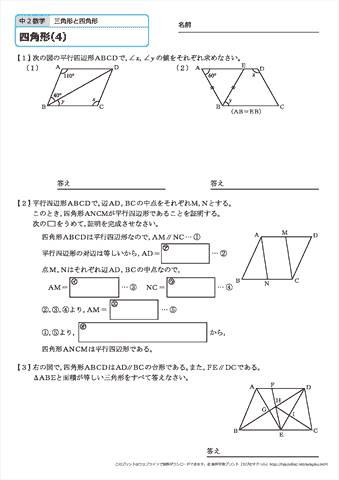



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
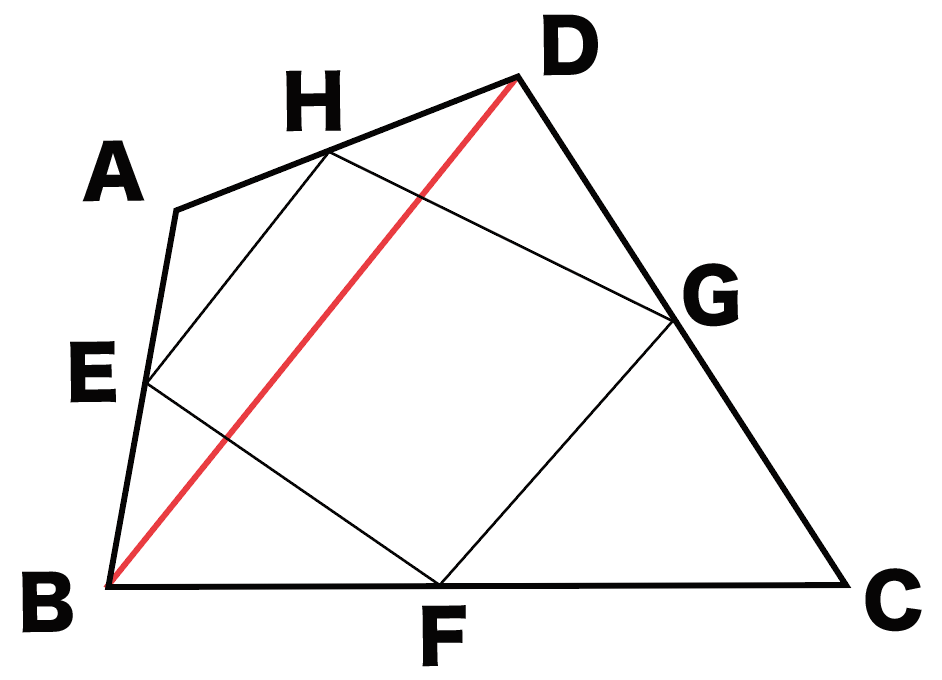



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の証明と角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中2 数学 平行四辺形になるための条件 なんでこうなるのかが わかりません Clear



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
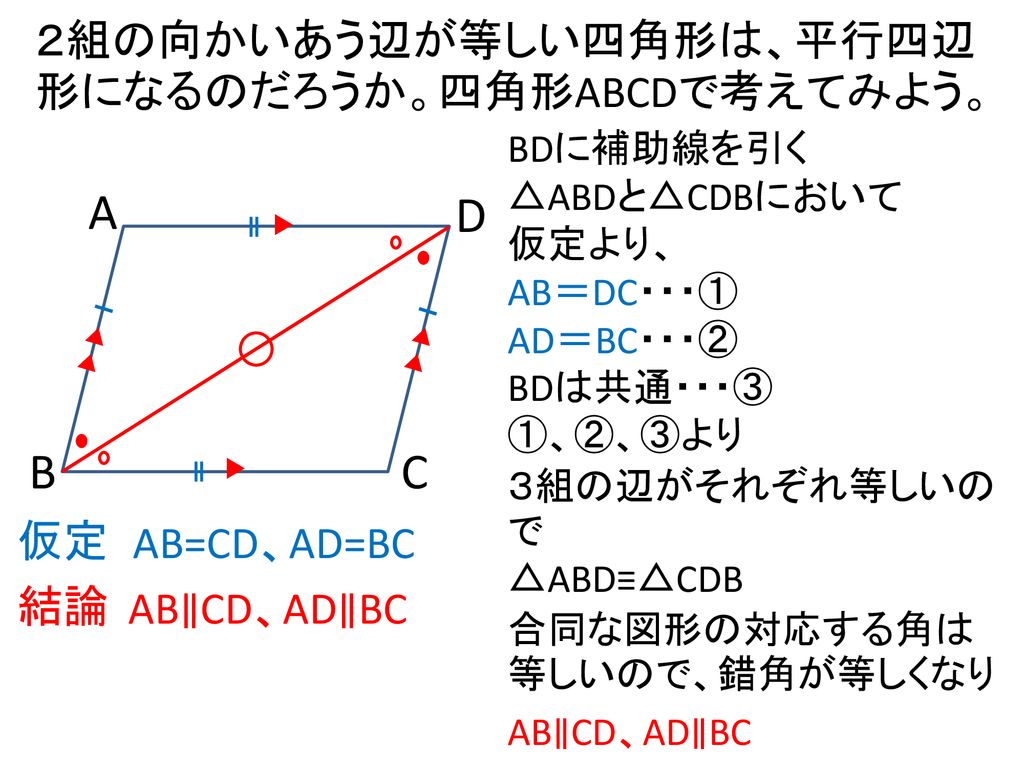



ねらい 平行四辺形の性質の逆を証明し 平行四辺形になるための条件を導くことができる Ppt Download
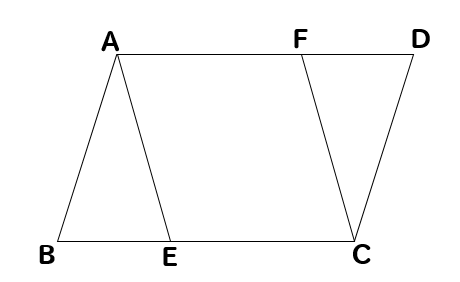



中学数学 平行四辺形の証明問題を徹底解説 数スタ
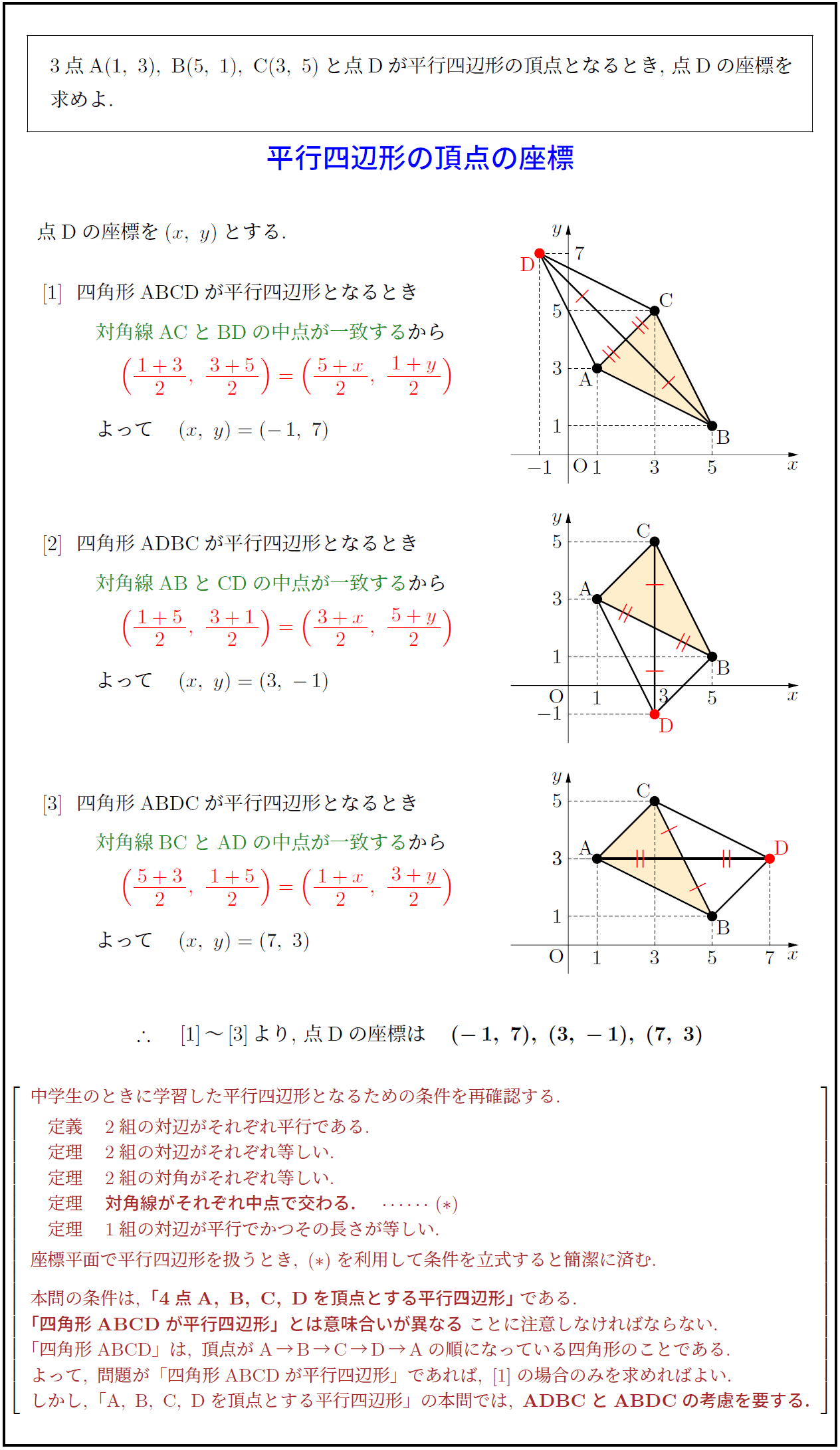



高校数学 平行四辺形の頂点の座標 受験の月




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題
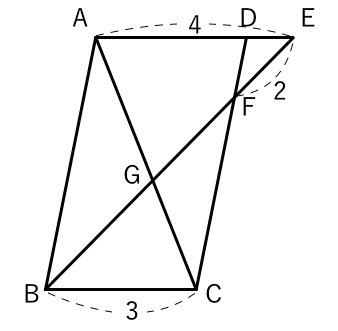



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



1




ベクトルの外積と平行四辺形の面積 身勝手な主張
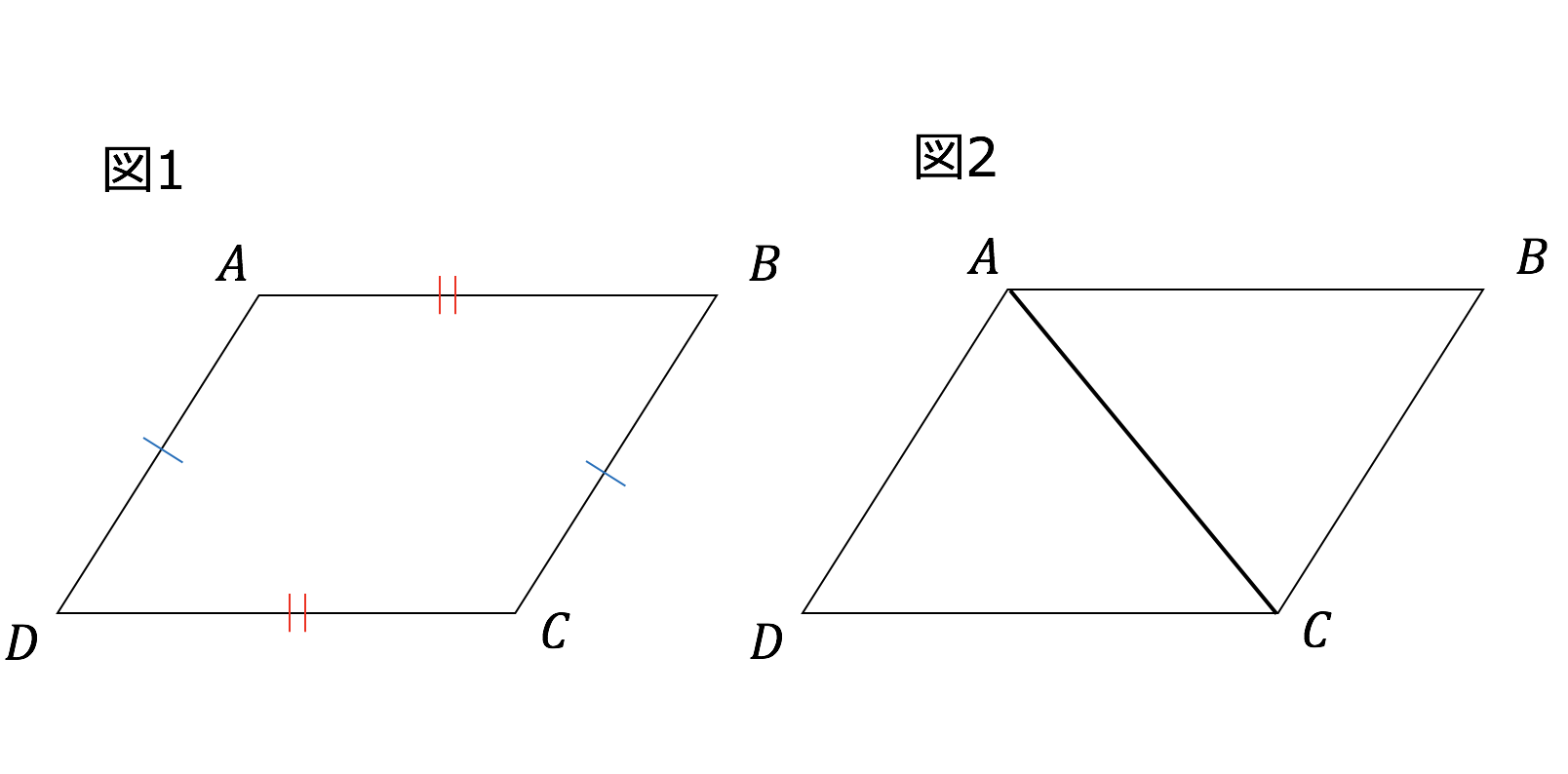



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
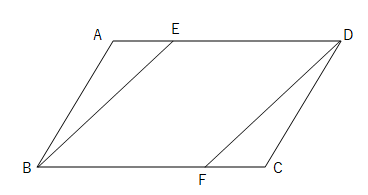



中2数学 平行四辺形の証明のポイントと練習問題 Examee




平行四辺形を使った証明 Youtube
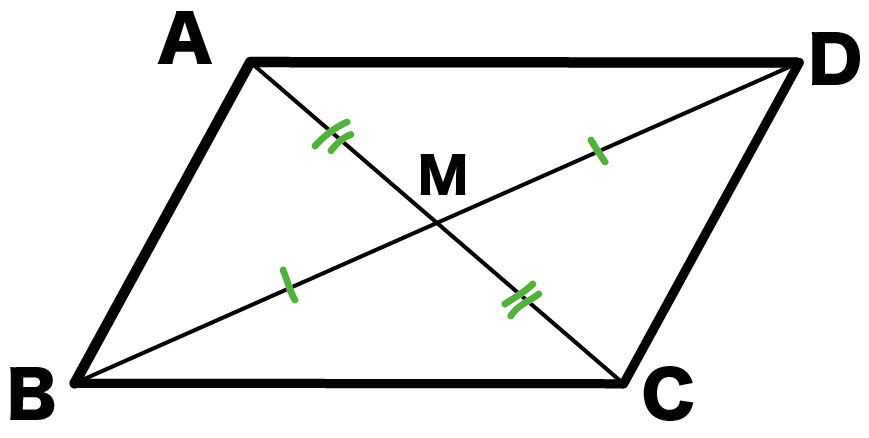



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




平行四辺形の証明問題 無料で使える中学学習プリント
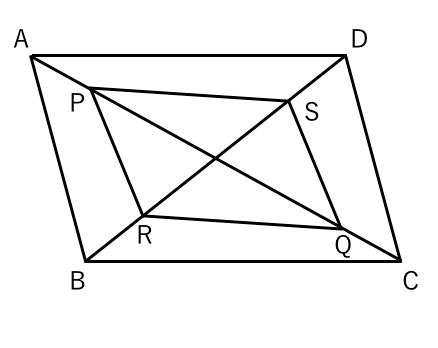



平行四辺形であることを証明する 苦手な数学を簡単に




中学数学 平行四辺形の証明問題が誰でもできるようになる方法 平行四辺形と辺を共有する問題 中2数学 Youtube



0 件のコメント:
コメントを投稿