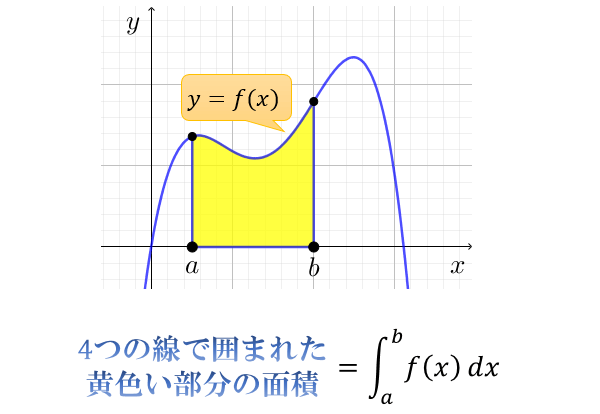
球冠,球帯の面積の求め方02 球をある平面で切り取った部分, 球冠 ,の表面積は,以下の図で示すように, 積分範囲を,0からl 2 までにすればよいので, と表すことができます.面積積分について (注意:元に戻るとき,ブラウザの戻るボタンを使わないように) Ⅰ.積分 「積分とは微少量の足し算である」とも言える.例えば,関数 f (x) (以下では単に f と表す)の積分 は横軸に x をとり,縦軸に f を取ったとき,直線 x = a と f と直線 x = b と x 軸で囲まれた部分円の面積 円の面積 円の面積は、「円周率×半径×半径」により与えられる。 日本の小学校では、小学4年で、 面積の概念を学習して正方形や長方形の面積を求め、小学5年で、ようやく、平行四辺形 の面積を学んだあと、その延長線上で、円の面積が教えられる。 もっとも、小学校では、「半径×半径×3.14」(実際に計算する場合は、半径×半径×3 と概数計算を
面積を求めてみよう
円 面積 積分 一部
円 面積 積分 一部-上 円 面積 積分 一部 ピクチャー 球欠,球台の体積と球冠,球帯の表面積 高校数学の美しい物語底面の円の直径方向に座標軸 をとり, の範囲で断面を求めて積分する. 底面の円に描いた黄色の直角三角形で,斜辺の長さは半径 に等しいから, 次に高さ は, のとき で傾きが の直線上にあるから, ここで は奇関数の積分だから0 は上半円の面積だから



微分でつなげる円や球の公式 すうがくブログ 式変形ch
曲線の長さ → 携帯版は別頁 閉曲線で囲まれた図形の面積3(媒介変数表示) 例1 a>0, b>0, 0≦t≦2π のとき, x=a cos t , y=b sin t で囲まれた図形の面積を求めてください. (解答) 曲線の概形を描く (1) t の変化に対応した x, y の増減を調べる.この項目は、不定積分の公式、定積分と面積を参照してください。 例1. , のグラフが、 の範囲で囲む部分の図形の面積を求める。 解答 として、∴ , ∴ 面積を求める部分は、右図で黄色に塗られた部分。 , のグラフは、 に関して対称だから、求める面積sは、 において、両グラフが囲むそこで、積分方向を変えてみることにする。 ③球の表面積の公式の求め方(2) 表面積の変化量が一定になるように、積分方向を 変えて、球の表面に沿って積分するように計算して みることにする。 図2において円周を球の表面に沿った l 方向に積分 すると
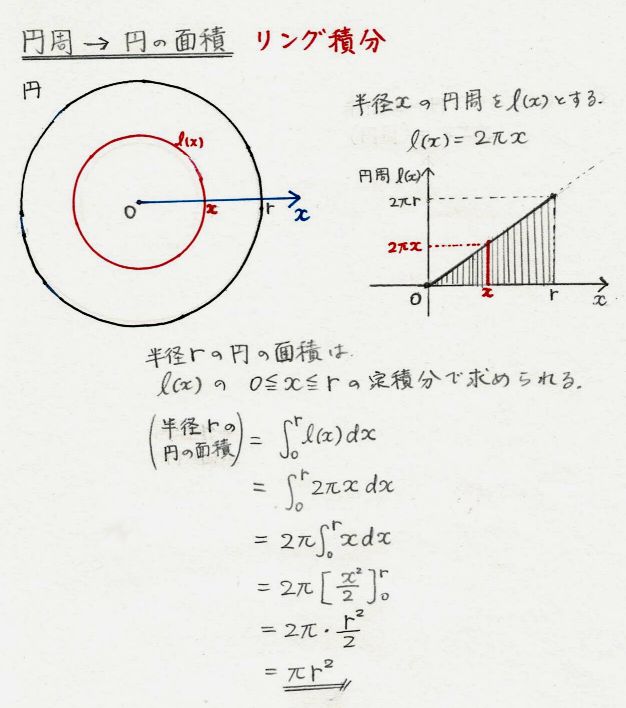
微分積分を使ってたような気がするんですが。。 例えば まずX軸Y軸があります。 その交点(座標で言うと(0,0)です)を中心にして 半径10cmの円があります。皆さんは、円の面積が $$$ S = \pi r^2 $$$ となることを知っていると思います。小学校か中学校で習ったでしょう。 では、なぜ円の面積が $$$ S = \pi r^2 $$$ となるかわかるでしょうか。 実はこの公式は積分計算で導くことができるんです。(円の面積) = π r 2 という公式が作られる。 円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。
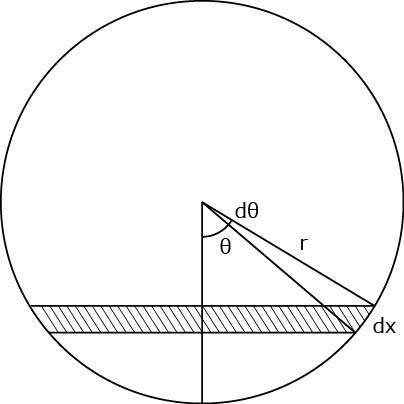
(2) その角度θ内の部分円の面積 Sc (mm^2) は、 Sc = (250^2)* (θ/2) = (250^2)*arctan (L/250) (3) その角度θ内の三角形の面積 St (mm^2) は、 St = 50*Lここで, r sin θ = h r\sin\theta=h rsinθ = h と置換すると, d h d θ = r cos θ \dfrac {dh} {d\theta}=r\cos\theta dθdh = rcosθ より, S = 2 π r ∫ h 1 h 2 d h = 2 π r h S=2\displaystyle\pi r\int_ {h_1}^ {h_2}dh=2\pi rh S = 2πr∫ h1円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体
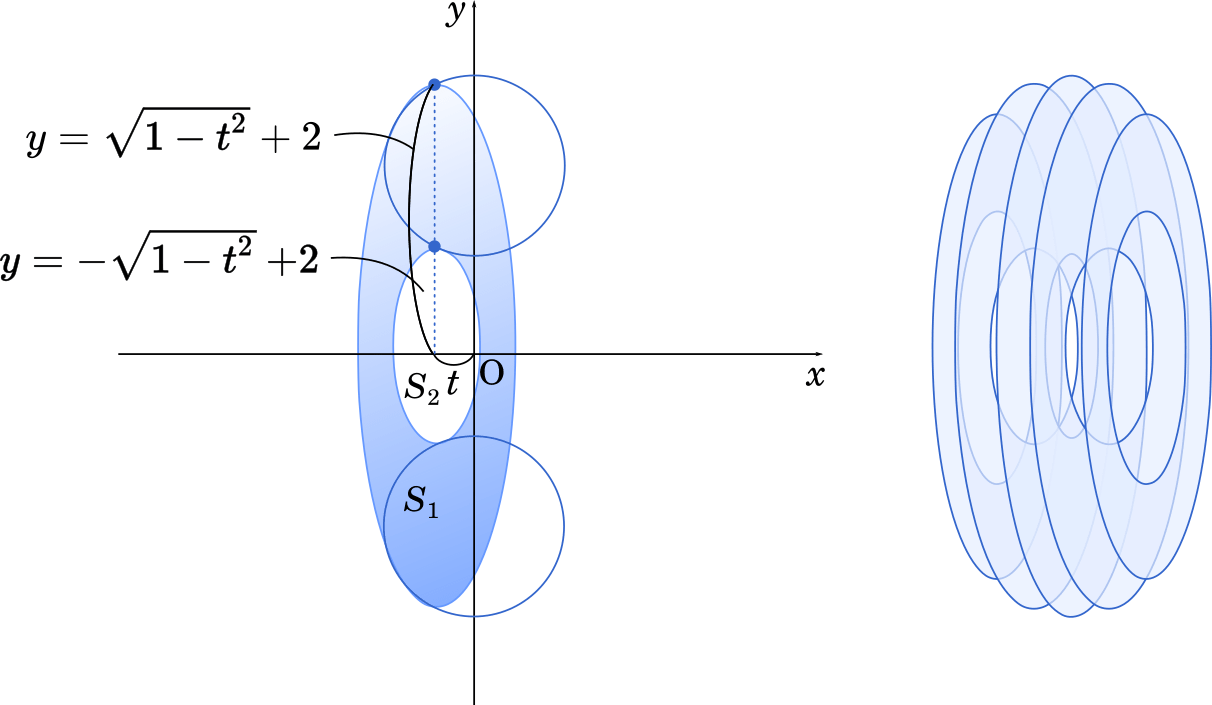



数iii積分 円環体 ドーナツ型 の体積の求め方 Mm参考書




半円を回転させる面積の問題 プリントを使って自分で解こう
円弧面積の計算式 扇形面積=円の面積×( 扇の内角/360°) 三角形の面積=( 半径 2 扇の面積-三角形の面積=円弧の面積 WingneoのIAの計算方法 円弧の始点・終点2点の座標値を丸める。「円弧面積の弦長を求める為の座標丸め」 その2点間距離を求める平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから)ここでは球の一部を考える. 答があっていることを確認しよう.積分を用いると容易に計算できる. は円の面積すなわち円周率$\pi$に興味を持っていたことがわかる.すなわち ,命題1は円の面積を渦巻き線の囲む面積に帰着させ(その面積を3倍すれ
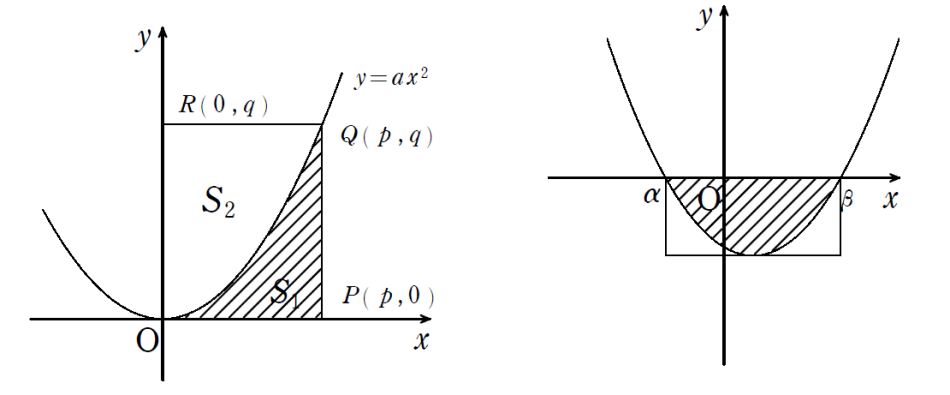



図形を利用した定積分の計算 授業実践記録 数学 高等学校 知が啓く 教科書の啓林館



Nkusuhashi Lecture Note
A=面積 A=ab a=A÷b b=A÷a (備考)a寸法はb辺に対し 直角に測ったもの A=面積 A=π(R 2r 2)=π(Rr)(Rr) =(D 2d 2) =(Dd)(Dd) A=面積 A=面積 A=面積 もし とすれば A=面積 A=面積 もし とすれば A=面積 P=楕円の周囲 A=πab 、Pを求める近似式 A=面積 A=面積BCD A=面積円の面積を,底辺r で高さ の直角三角形の集 積とみると, となる。なお,極座標 で円の極方程式を考えても,円の面積を求める式は である。 さらに,センターラインの公式やパップスギュルダ積分を利用して面積を求めるときは,どの曲線とどの曲線に囲まれているか,そして,曲線の上下関係を押さえることがポイントです。 特に, x 軸と曲線で囲まれる図形の面積は上下関係を忘れやすいので, x 軸を直線 y =0と考えるとよいでしょう。




微分でつなげる円や球の公式 すうがくブログ 式変形ch
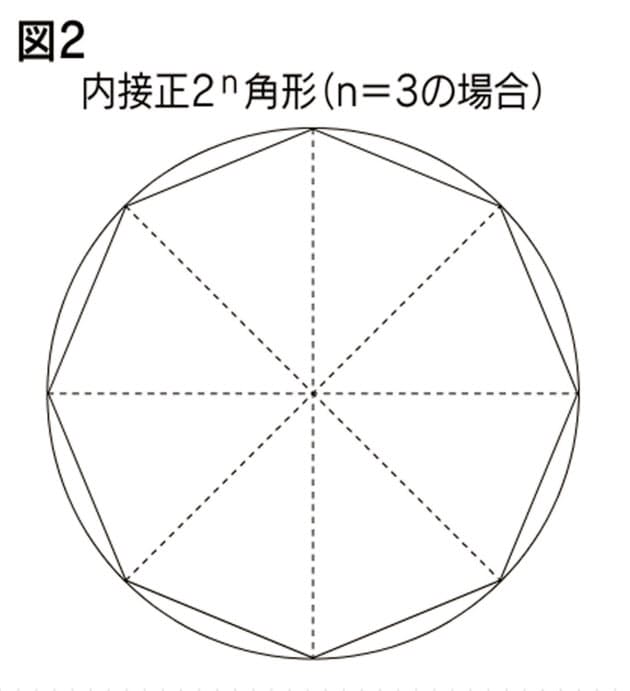



子供に説明できる 円の面積の公式 の証明 Nikkei Style
球の一部分の表面積を求めるには,積分が必要となります. そこで,まずは球そのものの表面積を計算しましょう. こちら,こちら,のサイトを参考にしました.特に,こちら,のサイトでは計算方法がよくわからなかったので,独自に計算してみました. まずは上記の図を用いて考えましょう. 球の表面積は,半径,y,の円に微小な厚みをかけた円帯を 円の部分面積と部分円周を教えてください。 添付にある円のCの面積と赤色で示しているBの寸法の計算での出し方がわかりません。 わかっているのは直径のDと円周から中心に向かっての長さAです。 考えます。 この面積の計算がわかれば奥行をかけて体積が出ます。 例えば直径Dが3000mmとし、Aが0mmとしたときに、Cの面積とBの長さを知りたいのです。 どなたか (1)円の面積を求める式、半径×半径×314にあてはめて、円の面積=3×3×314=26 (2)まず、半径の長さを先に求める。 半径は直径の半分だから、10÷2=5cm。 これを円の面積を求める式、半径×半径×314にあてはめて、円の面積=5×5×314=785




高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット




円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo
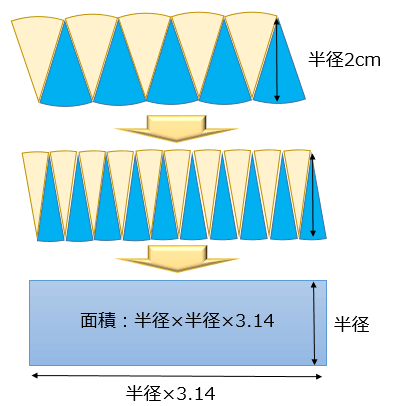
よって,面積は π ⋅ a ⋅ a \pi \cdot a\cdot a π ⋅ a ⋅a となり楕円の面積公式は確かに正しいです。 つまり,楕円の面積公式は円の面積公式を含んでいます。 中心が原点でない楕円の面積も求めることができます。 例 楕円 ( x 10) 2 9 ( y − 1) 2 16 = 1 \dfrac { (x10)^2} {9}\dfrac { (y 極方程式の面積公式発展 極方程式で表された曲線の面積は,定積分で次のように求めることができます。 極方程式の面積公式 極方程式 r = f (\theta) \ (\alpha ≦ \theta ≦ \beta) ( ) で表される曲線上の点と極 O を結んだ線分が通過する領域の面積は 半径 の円の円周の長さは2 、これは円周率の定義でもあるが、円を円の中心を頂点とする二等辺三角形に分割して考えれば、円の面積は、積分を用いなくても、円周×半径÷2として簡単に求めることができる。 しかし、ここでは、微積分を学習する意味から、あえて積分して求めることにし



円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ




くろべえ 卵焼きの失敗と 2円の重なり部分の面積
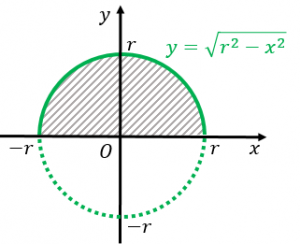
まず、円は原点中心、半径aの円なので、X軸よりも上側の円周は、次の式で表されます。 x^2+y^2=a^2 移項してyについて解くと y=√(a^2-x^2) (今はx軸の上側だけ考えているので『±』は付けません) よって,面積Sを求める積分の式は S=2∫ (a~k){√(a^2-x^2)}dx ・・・ (1) (aが下で,kが上です) (ただの積分だと上だけ求めて終わりになってしまうので、2倍し一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積 楕円柱の体積 直円錐の体積 斜切円錐の体積 一部が欠けた直円錐の体積 円錐台の体積 楕円錐の体積 楕円錐台の体積 球の体積 一部が欠けた球の体積 弓形の回転体の体積 一部が欠けた弓形の回転体の体積球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる
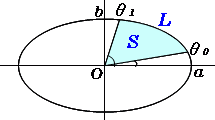



楕円扇形の面積 高精度計算サイト
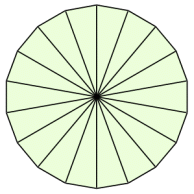



積分 円の面積の再考 大人が学び直す数学
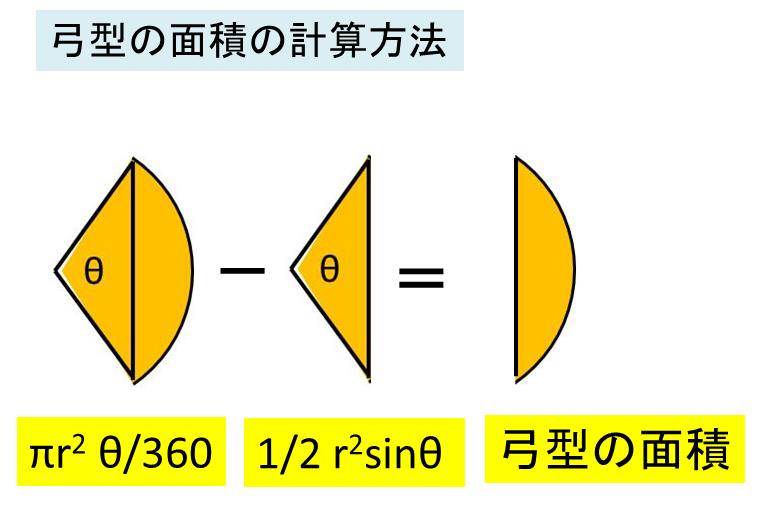
弓形の面積 弓形とは円とその割線 (円と異なる二点で交わる直線)で囲まれる図形で、図1における網掛け部分のような図形です。 実はその反対側も弓形です。 以下では弓形の面積をS、円の半径をr、弓形の基になる扇形の中心角をθとします。 但し、中心その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。 円の面積の積分を式で表してみると、 ∫√(r 2 -χ 2 )dx である。No011 弓形の面積と円弧の長さ A:弓形の面積 m 2 ,l:弓形の円弧の長さ m,r:弓形の半径 m,θ:弓形の角度 °



面積を求めてみよう




標準 おうぎ形と正方形の面積 なかけんの数学ノート
いろいろな図形上の面積分 = 1 0 1y 0 f (x, y)dxdy T f dS = 1 0 1x 0 f (x, y)dydx y 1 y x y 1 1 0 x 1 x T x y 1 1 0 T 例.三角形 T = {(x, y) x y 1, x, y ⇥ 0} 上の積分 面積分 f dS の計算は適当な座標軸に沿った2回の積分を実行 することによって行う. Ex33第14回 基礎数学Ⅱ 1月28日(火)3時限目(1300~1430) m6 概要 置換積分法・部分積分法と2つの曲線で囲まれた部分の面積について 補足、 問14 キーワード 定積分の置換積分法、定積分の部分積分法、2つの曲線で囲まれた部分の面積、回転体の体積、回転体の表面積積分法についての理解を深めるとともに,その有用性を認識し,事象の考察に活用できる ようにする。 本事例では,微分・積分の考え方を理解することで,円の面積と長さ,球の体積と表面積の関係に ついて考察させることを意図している。




円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ
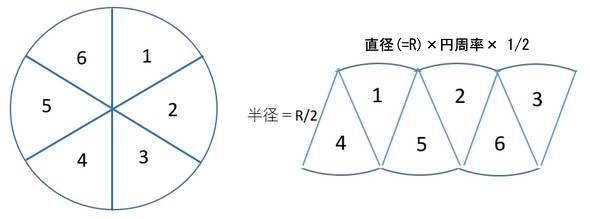
高校の数学2や数学3で学ぶ積分は、不定積分ができるものに限って問題が作ら れています。では、不定積分が簡単に求められない場合はどうすればよいのでしょ うか。ここでは面積の計算を通して数値積分のやり方を検討してみましょう。 まず、円の面積を求めることを考えます。「微分・積分」の勉強 (1)積分: 以下の問題を考えます。 問題 半径 1 の円の面積Sをπと定義する。 面積S=π この面積Sを求めよ。 (解答) この問題は、以下の様に解くことができます。 円を、以下の図の様な短冊に分割し、 その 図1のように円を木の年輪のように考え これを半径で切って広げると図2のような形になります。 年輪を細かくすればするほど図3のように三角形に近い形になります。 底 辺の長さは円の ( ①)と等しく、高さは (②)と等しいので (三角形の面積)= (底辺)× (高さ)÷2 (円の面積) = (①)× (②)÷2 = (直径)× (③)× (②)÷2 = (直径)÷2× (②)× 算数 数学について、n×nの正方




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ



切頭円柱の体積の小手技
ベストアンサー 半径aの円の方程式はxy軸で表現すると x²y²=a² よって、 y=±√ (a²x²) です。 面積は∫ydxだから、 a ∫√a²x²)dx a の2倍です。 この ∫√ (a²x²)dx の計算の仕方が、 置換積分 x=acosθ もしくは、x=asinθとするわけです。 x=acosθとすると、 dx/dθ=asinθ dx=asinθdθ √ (a²x²) =√a² (1cos²θ) =asinθ だから、 定積分範囲は、 x=aのとき1=cosθだから、θ=π x=aの円の面積 πr 2 を微分 一部誤差はありますが、一面に張り付けられます。 (先ほどの紙風船の場合は逆にのりしろの部分をはがしていけばよいのです。 区分求積法の概念ができていれば、 「円周を積分→円の面積」「球の表面積を積分→球の体積円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S




円 扇形 の面積 周や弧の長さの公式 数学fun



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
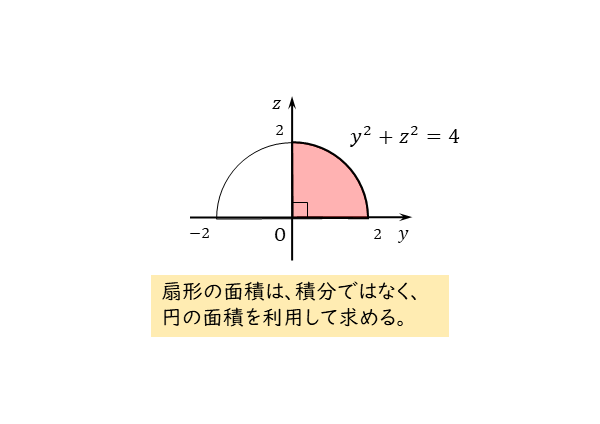



数学3 回転体を扱った入試問題を解いてみよう 日々是鍛錬 ひびこれたんれん



数学 温故知新ラーニング 楽天ブログ
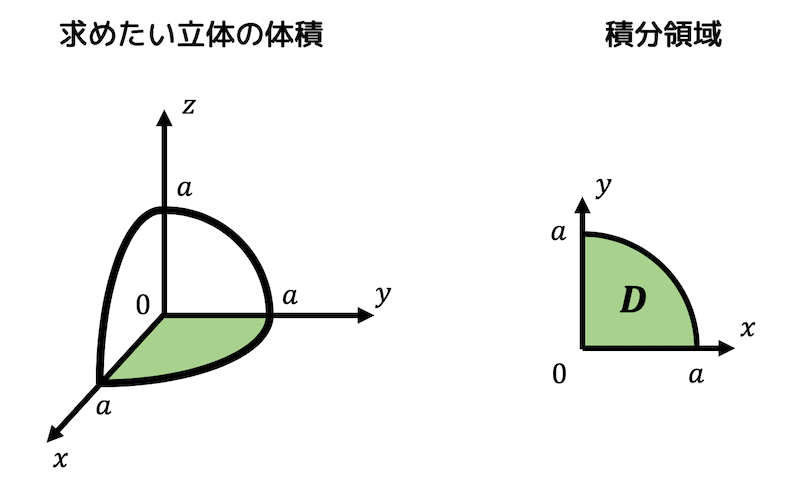



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾
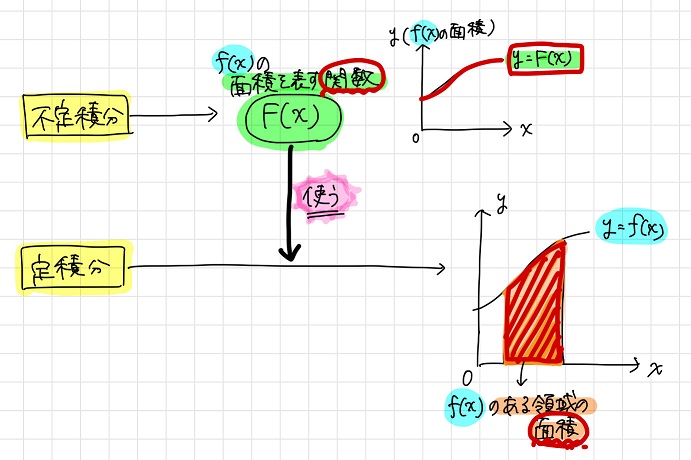



微分積分 定積分と不定積分の違いや関係性 それぞれの特徴とは 積分定数にも着目して解説します 黒豆納豆の特許翻訳
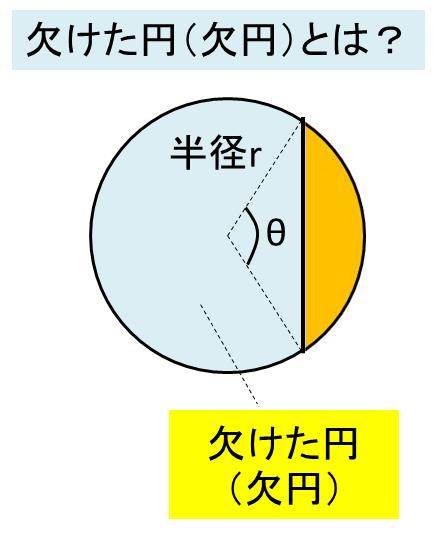



欠けた円 欠円 や弓形の面積の計算方法



円の一部の一部の面積を求める式が知りたいです 円の一部の面積を求めることはでき Yahoo 知恵袋




弓形の面積 香料ゐっすゐの夢



円の面積



この積分が半円の面積を示しているのは何故でしょうか Yahoo 知恵袋



添付のような2つの円の交わった部分の面積の求め方を教えて下さい 2つの Yahoo 知恵袋



問題93おうぎ形の面積
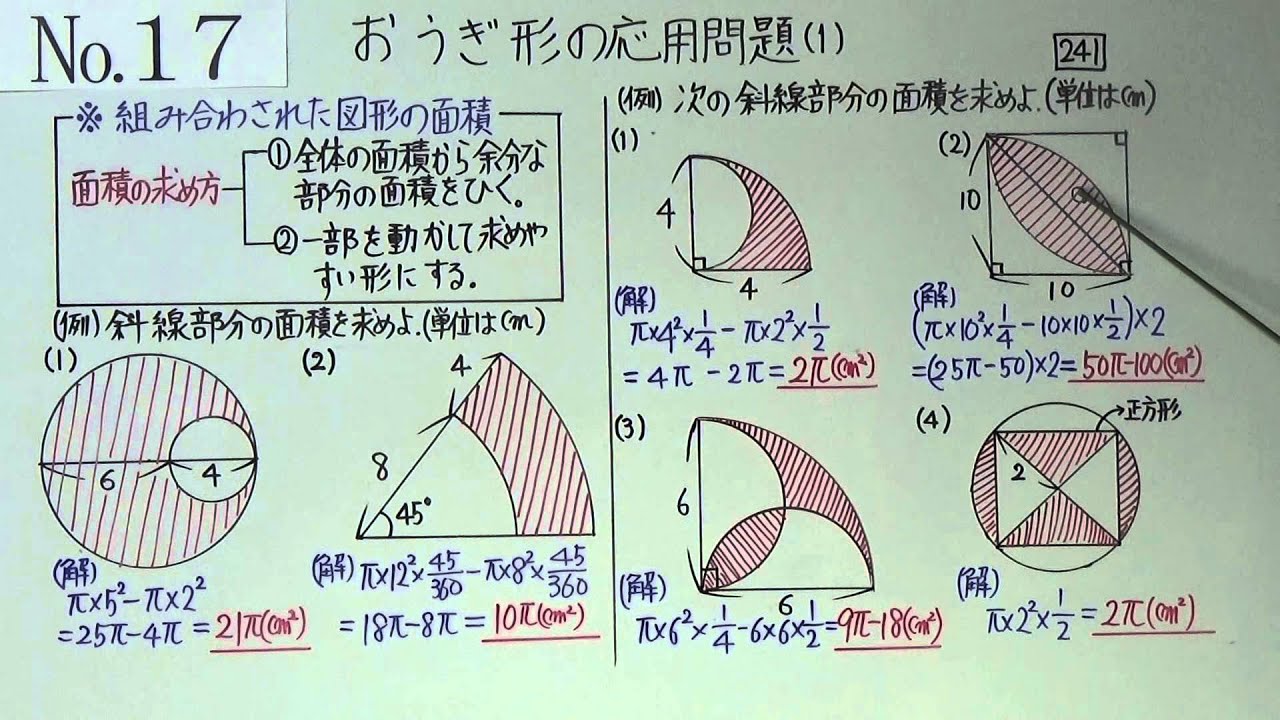



中1 17 2 おうぎ形の応用 1 Youtube




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
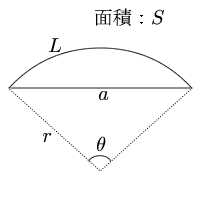



弓形 面積の計算 計算サイト
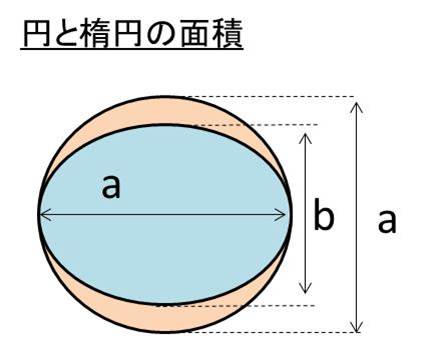



X Acos8とy Bsin8の面積の計算方法は 楕円の面積の一部の求め方は 楕円の面積と円の面積 ウルトラフリーダム
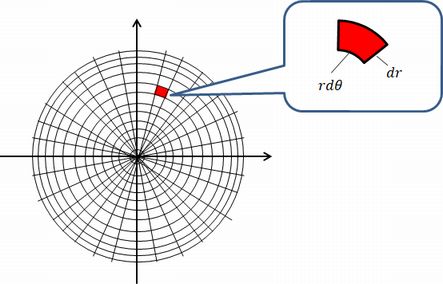



極座標で円の面積を求める方法の補足 おにノート おーにしの物理 数学ノート




極方程式の面積 扇形積分 おいしい数学




角錐 円錐の体積と表面積の公式 数学fun




高校数学 媒介変数表示で表される曲線で囲まれた部分の面積 リサジュー曲線 受験の月



積分の結果って本当に面積になるの プログラミングの力で検証してみた モンテカルロ法 自主的 るぅる




高校数学 楕円の面積と回転体の体積 受験の月



円の面積の求め方 小学生



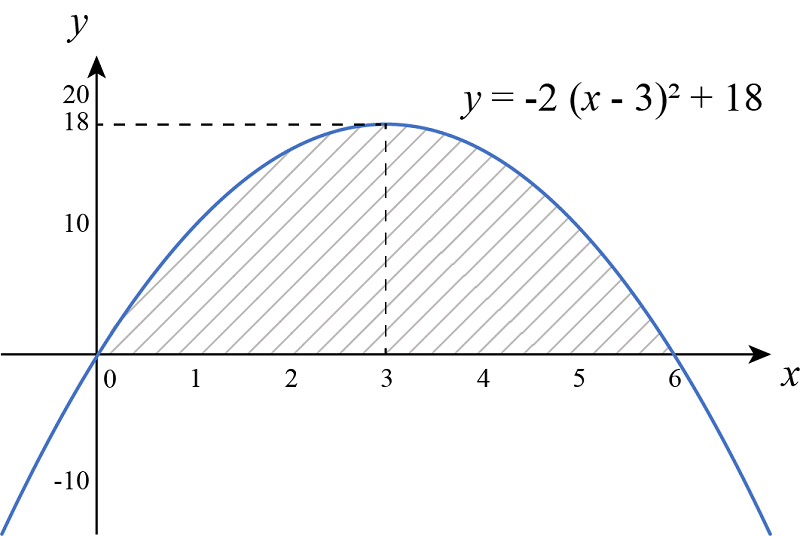
円と放物線に囲まれた面積 微分法と積分法 おおぞらラボ




15年度 愛光中学校 算数 1 6 面積
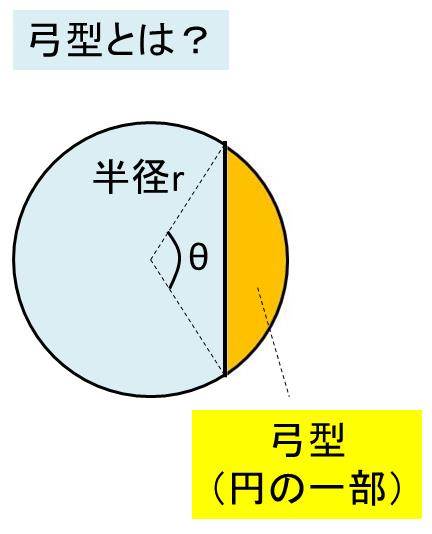



欠けた円 欠円 や弓形の面積の計算方法
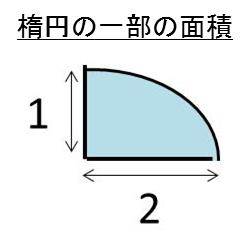



X Acos8とy Bsin8の面積の計算方法は 楕円の面積の一部の求め方は 楕円の面積と円の面積 ウルトラフリーダム




くろべえ 卵焼きの失敗と 2円の重なり部分の面積



積分 続き



1




高校数学 特殊な置換をする定積分 A X を含む定積分はx Asin8とおけ 受験の月




標準 楕円で囲まれた部分の面積と積分 なかけんの数学ノート



円の面積



コロキウム室 円に関する微分



面積分 例題



円の一部の面積と 円の直径があり これらの情報から Xの距離を求 Yahoo 知恵袋




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾
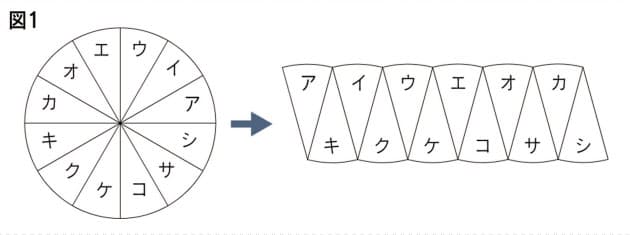



子供に説明できる 円の面積の公式 の証明 Nikkei Style




高校生向け 積分 円の面積 Youtube




扇形の面積の求め方 公式と計算例



48s96ub7b0z5f Net Houbutsusen En Menseki




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



欠けた円 欠円 や弓形の面積の計算方法



P 3 05を証明せよ 東大の伝説の入試問題をプログラムで解く 組み込みエンジニアの現場力養成ドリル 27 3 5 ページ Techfactory




領域 連立不等式の範囲を図示する方法と格子点と面積の求め方




円の面積 Area Of A Circle Youtube




積分法の話題3 放物線と円とで囲まれた部分の面積 高校数学 身勝手な主張



円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ




高校数学 定積分と面積 2 問題編 映像授業のtry It トライイット




中学校入試問題 算数 解いてください 半径9cmの円 を4分の1 に Okwave



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



1 6公式の使い方 思考力を鍛える数学
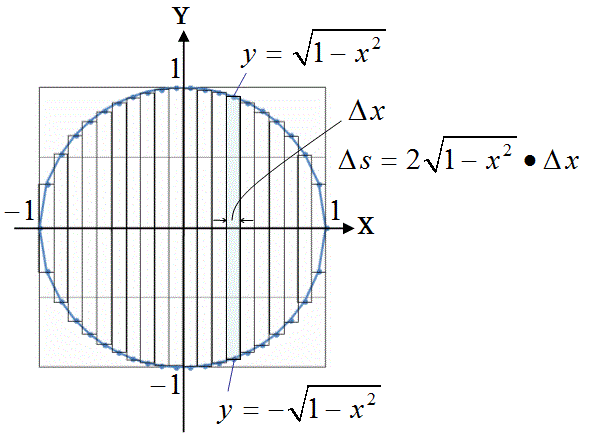



勉強しよう数学 円の面積を積分で求める



球帯と球冠




アルゴリズム 2つの円の重なった面積 Teratail




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




球の体積 球の表面積の公式の導出 積分 優技録



面積分



円の面積を積分で計算する2通りの方法 具体例で学ぶ数学
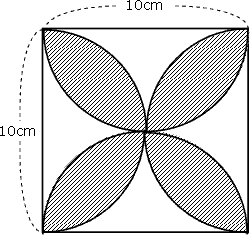



面積の求め方 算数の教え上手 学びの場 Com



Object 01
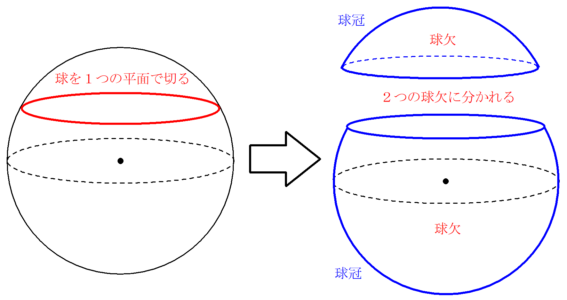



球欠と球冠 Fukusukeの数学めも




円の面積の求め方 公式と計算例




極方程式の面積 扇形積分 おいしい数学




楕円の知識まとめ 面積 方程式 焦点 接線 媒介変数表示 理系ラボ
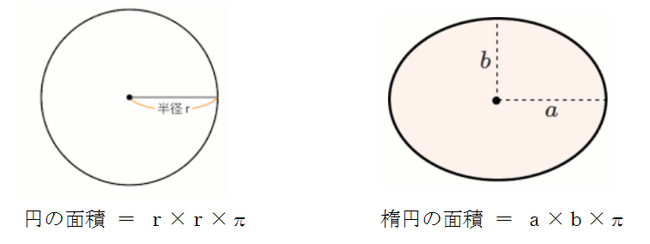



楕円の面積の公式 小学生でもわかる計算問題を紹介するぞ 三重の個人契約家庭教師




絶対値記号を含む定積分 数学 苦手解決q A 進研ゼミ高校講座
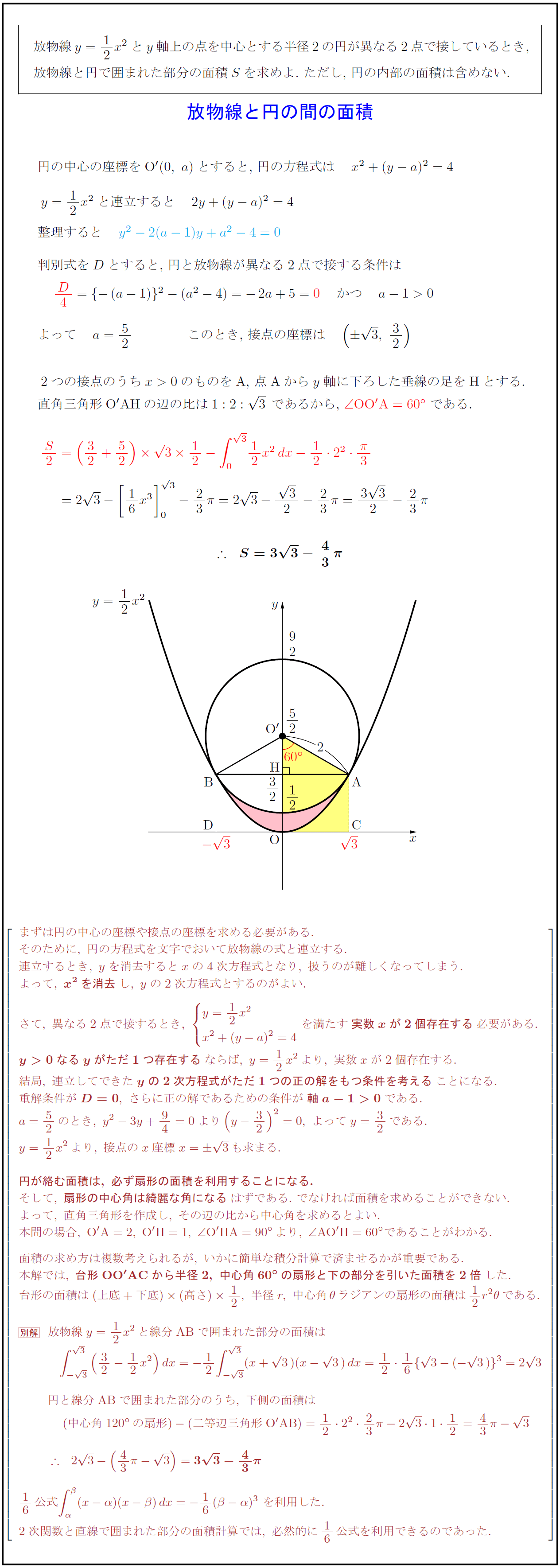



高校数学 放物線と円の間の面積 受験の月



48s96ub7b0z5f Net Houbutsusen En Menseki




積分法の話題3 放物線と円とで囲まれた部分の面積 高校数学 身勝手な主張



3




中学受験の算数 面積の問題 わからないので教えてください よろしくお願い Okwave




弓形の面積 香料ゐっすゐの夢




微分でつなげる円や球の公式 すうがくブログ 式変形ch




はっぱ型 の図形の面積 身勝手な主張



微積分公式 京極一樹の数学塾




斜線の部分の面積を求めなさい 上の図は 半径10センチメートルの円の半 Okwave



大学入試問題




2つの円の一部が重なった図 2つの同じ大きさの円の一部が重なった状 数学 教えて Goo



積分法 佐々木数学塾




円の面積の公式 算数の公式
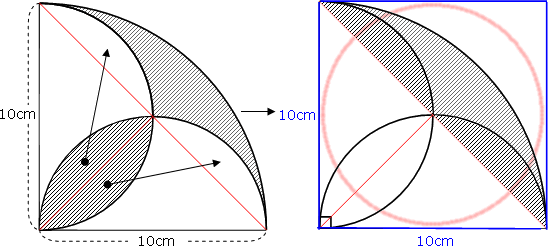



面積の求め方 算数の教え上手 学びの場 Com




円の面積 練習応用 Youtube
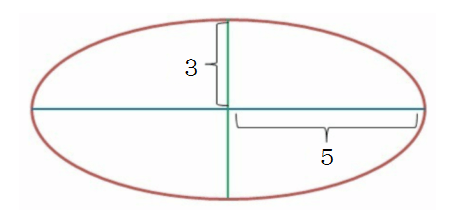



楕円の面積の公式 小学生でもわかる計算問題を紹介するぞ 三重の個人契約家庭教師



0 件のコメント:
コメントを投稿